加窗函数 - 理解FFT和信号加窗原理及意义

admin

http://www.elecfans.com/emb/fpga/20171116580796_3.html

[color=rgb(51, 51, 51) !important]窗的波形图显示了窗本身为一个连续的频谱，有一个主瓣，若干旁瓣。 主瓣是时域信号频率成分的中央，旁瓣接近于0。 旁瓣的高度显示了加窗函数对于主瓣周围频率的影响。 对强正弦信号的旁瓣响应可能会超过对较近的弱正弦信号主瓣响应。 一般而言，低旁瓣会减少FFT的泄漏，但是增加主瓣的带宽。 旁瓣的跌落速率是旁瓣峰值的渐进衰减速率。 增加旁瓣的跌落速率，可减少频谱泄漏。

[color=rgb(51, 51, 51) !important]选择加窗函数并非易事。 每一种加窗函数都有其特征和适用范围。 要选择加窗函数，必须先估计信号的频率成分。

[color=rgb(51, 51, 51) !important]如果您的信号具有强干扰频率分量，与感兴趣分量相距较远，那么就应选择具有高旁瓣下降率的平滑窗。

[color=rgb(51, 51, 51) !important]如果您的信号具有强干扰频率分量，与感兴趣分量相距较近，那么就应选择具有低最大旁瓣的窗。

[color=rgb(51, 51, 51) !important]如果感兴趣频率包含两种或多种很距离很近的信号，这时频谱分辨率就非常重要。 在这种情况下，最好选用具有窄主瓣的平滑窗。

[color=rgb(51, 51, 51) !important]如果一个频率成分的幅值精度比信号成分在某个频率区间内精确位置更重要，选择宽主瓣的窗。

[color=rgb(51, 51, 51) !important]如信号频谱较平或频率成分较宽，使用统一窗，或不使用窗。

[color=rgb(51, 51, 51) !important]总之，Hanning窗适用于95%的情况。 它不仅具有较好的频率分辨率，还可减少频谱泄露。 如果您不知道信号特征但是又想使用平滑窗，那么就选择Hanning窗。

[color=rgb(51, 51, 51) !important]即使不使用任何窗，信号也会与高度一致的长方形窗进行卷积运算。本质上相当于对时域输入信号进行截屏，对离散信号也有效。 该卷积有一个正弦波函数特性的频谱。 基于该原因，没有窗叫做统一窗或长方形窗。

[color=rgb(51, 51, 51) !important]Hamming窗和Hanning窗都有正弦波的外形。 两个窗都会产生宽波峰低旁瓣的结果。 Hanning窗在窗口的两端都为0，杜绝了所有不连续性。 Hamming窗的窗口两端不为0，信号中仍然会呈现不连续性。 Hamming窗擅长减少最近的旁瓣，但是不擅长减少其他旁瓣。 Hamming窗和Hanning适用于对频率精度要求较高对旁瓣要求较低的噪声测量。

[color=rgb(51, 51, 51) !important]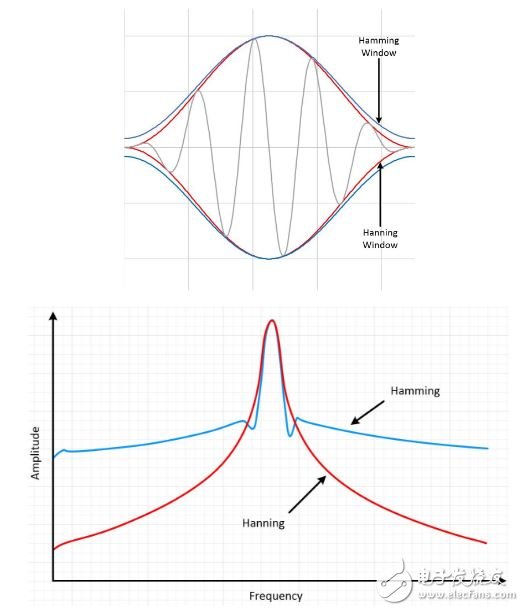

[color=rgb(51, 51, 51) !important]图13： Hamming和Hanning都会产生宽波峰低旁瓣的结果。

[color=rgb(51, 51, 51) !important]Blackman-Harris窗类似于Hamming和Hanning窗。 得到的频谱有较宽的波峰，旁瓣有压缩。 该窗主要有两种类型。 4阶Blackman-Harris是一种通用窗，在高90s dB处具有旁瓣抑制功能，有较宽的主瓣。 7阶Blackman-Harris窗函数有宽广的动态范围，有较宽的主瓣。

[color=rgb(51, 51, 51) !important]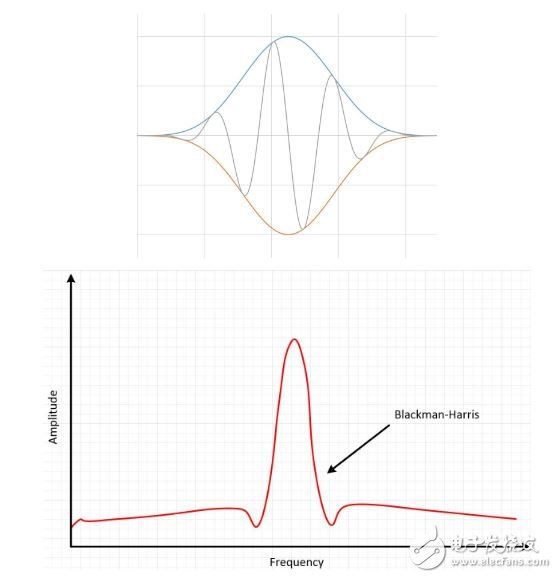

[color=rgb(51, 51, 51) !important]图14： Blackman-Harris窗的结果是较宽的波峰，旁瓣有压缩。

[color=rgb(51, 51, 51) !important]Kaiser-Bessel窗在幅值精度、旁瓣距离和旁瓣高度之间取得了较好的平衡。 Kaiser-Bessel窗与Blackman-Harris窗类似，对于相同的主瓣宽度而言，较近的旁瓣更高，较远的旁瓣更低。 选择该窗通常会将信号泄漏至离噪声较近的位置。

[color=rgb(51, 51, 51) !important]Flat top窗也是一个正弦波，穿过0线。 Flat top窗的结果是在频域中产生一个显著宽广的波峰，与其他窗相比离信号的实际幅值更近。

[color=rgb(51, 51, 51) !important]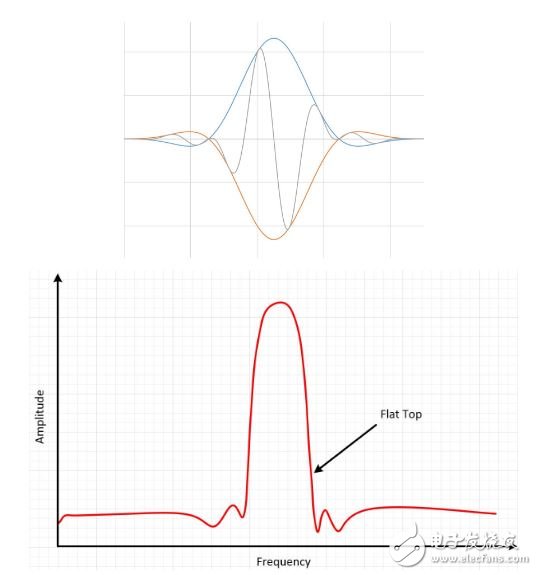

[color=rgb(51, 51, 51) !important]图15：Flat top窗具有更精确的幅值信息。

[color=rgb(51, 51, 51) !important]上面列举了几种常见的窗函数。 选择窗函数并没有一个通行的方法。 下表可帮助您做出初步选择。 请始终比较窗函数的性能，从而找到最适合的一种窗函数。

[color=rgb(51, 51, 51) !important]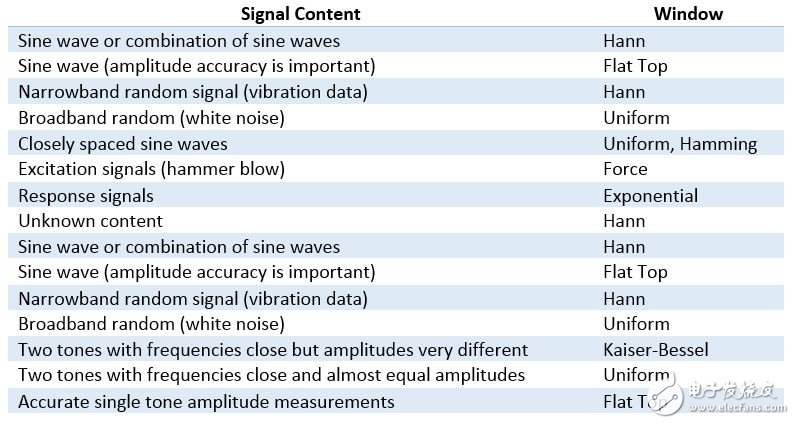

3. 总结

[color=rgb(51, 51, 51) !important]所有时域中的信号都可表示为一组正弦波。

[color=rgb(51, 51, 51) !important]FFT变换将一个时域信号分解为在频域中表示，并分析信号中的不同频率成分。

[color=rgb(51, 51, 51) !important]在频域中显示信号有助于发现信号中的干扰、噪声和抖动。

[color=rgb(51, 51, 51) !important]信号中如果包含非整数个周期，会发生频率泄漏。可通过加窗来改善该情况。

[color=rgb(51, 51, 51) !important]数字化仪采集到的有限序列的边界会呈现不连续性。加窗可减少这些不连续部分的幅值。

[color=rgb(51, 51, 51) !important]没有窗叫做统一窗或长方形窗，因为加窗效果仍然存在。

[color=rgb(51, 51, 51) !important]一般情况下，Hanning窗适用于95%的情况。 它不仅具有较好的频率分辨率，还可减少频谱泄露。

[color=rgb(51, 51, 51) !important]请始终比较窗函数的性能，从而找到最适合的一种窗函数。